In other words, to determine k′, Eve generates a chain of keys starting with Y 1 = R(c0) and up to the length t. If Alice computed c0 using a key that is contained in the table, then Eve will eventually generate the key that matches the last key (the endpoint) in the corresponding chain. As an example, if Alice’s key k′ is X22 in Figure 19.17, then calculating ft−2(X22) will result in a key equal to the endpoint E2.

Because the last key is stored with its corresponding first key (the starting point), Eve can recompute the entire key chain, including the key that comes just before R(c0), that is, the key that Alice used to compute c0.

However, because the reduction function R in Hellman’s method is an arbitrary reduction of the ciphertext space in the key space, it is possible that key chains starting at different keys will collide and merge. Each merge, in turn, reduces the number of keys that are covered by the table. Even worse, the probability that a new chain will merge with an existing one increases with the size of the table.

In 2003, the Swiss cryptographer Philippe Oechslin observed that it is better to generate multiple tables using a different reduction function for each table [134]. While collisions are still possible, the chains do not merge because different tables use different reduction functions.

Based on this observation, Oechslin proposed a new type of chain, which he referred to as rainbow chains. Rainbow chains can collide within a single table, but are very unlikely to merge [134] because they use a different reduction function Ri for every element in the key chain. As a result, if there is a collision between two chains, they will only merge if the collision appears at the same position in both chains. Otherwise, the chains will continue with a different reduction function and, thus, will not merge.

To find Alice’s key k′ in a rainbow table, Eve proceeds in the same way as with Hellman’s method, only using different reduction functions. To check whether c0 is an endpoints, she computes Rt−1. If one of the endpoints is equal to Rt−1, Eve uses the corresponding starting point to rebuild the key chain, in particular, the next to the last chain element. If none of the endpoints is equal to Rt−1, Eve checks whether k′ is in the second-last column using Rt−2,ft−1, in the third-last column using Rt−3,ft−2,ft−1, and so on.

But why rainbow chains and rainbow tables? During his presentation at the Crypto 2003 conference, Oechslin added colors to the original graphic from his paper. The colored graphic is shown in Figure 19.18 and explains the rainbow association.

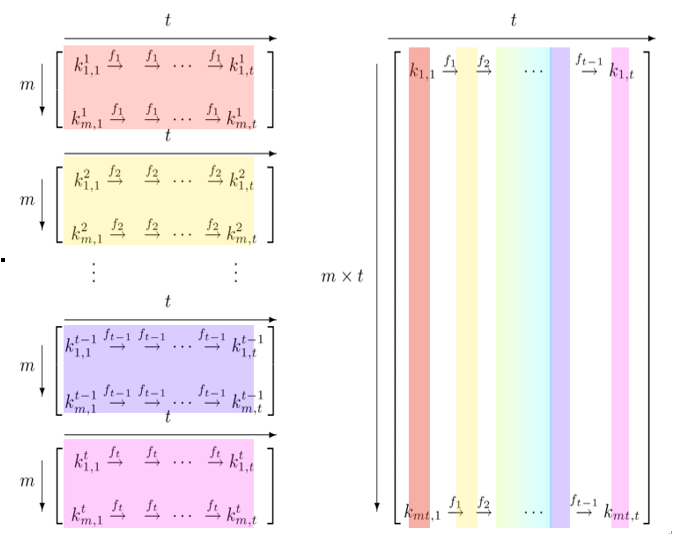
Figure 19.18: Colored graphic in Oechslin’s Crypto 2003 talk used to illustrate rainbow tables

19.8 Summary

In this chapter, we discussed common attacks on cryptography. We mostly focused on attacks relevant to cryptographic protocols such as TLS, that is, attacks that are independent of the underlying cryptographic primitives. We then complemented our discussion with attacks on symmetric and asymmetric encryption schemes and hash functions. The security of digital signatures, which are based either on RSA or on elliptic curves, relies on the security of these cryptographic primitives.

In the next chapter, we will cover actual, real-world attacks on the TLS Handshake protocol. The material covered in this chapter will make it easier for you to understand those attacks.