20.2 Logjam

Logjam (see [1]) represents the practical implementation of the attack template shown in Figure 20.1 with respect to the DHE key-establishment protocol. Here, the server is tricked into selecting a weak export-grade DHE cipher suite such as this:

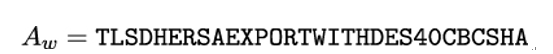
As discussed earlier, the client therefore receives weak key parameters and uses them to generate a shared secret that can be computed by Mallory, despite having negotiated a stronger cipher suite. The underlying weakness, the lack of early authentication of the cipher suite selected by the server, is resolved in TLS 1.3.

20.3 SLOTH

SLOTH [31] uses a weaker form of second-preimage resistance for a hash function h, namely chosen-prefix collision resistance. Given two prefixes P1 and P2, it should be computationally hard to find a pair of values x1,x2 so that

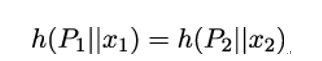
The use of MD5 and SHA-1 is mandated in TLS 1.0 and TLS 1.1 and is still possible in TLS 1.2. However, these older hash functions are not chosen-prefix collision resistant. This weakness can be used by an attacker either to manipulate the initial handshake messages in order to downgrade the negotiated cipher suites or to break client/server authentication. The possibility of these attacks leads to the deprecation of MD5-based signatures in TLS 1.3.

The attacker in this scenario is a man-in-the-middle with sufficient computing resources to generate the chosen-prefix collisions within a short time frame. The attack is based on the fact that, for example, the ClientHello can include extensions that the server does not understand or support and will consequently ignore. Similarly, ServerCertificateRequest can include an optional list of distinguished names of certificate authorities the server trusts. Again, such a list may include arbitrary data the client will ignore if it does not recognize them. These arbitrary parts give an attacker room to generate chosen-prefix collisions.

20.4 Padding oracle attacks on TLS handshake

The term oracle originally comes from complexity theory, where it is used to compare the complexity of two computational problems P1,P2.

Suppose we can solve P1 efficiently (i.e., in polynomial time), if there is a polynomial-time algorithm A to solve P2. In this situation, we say that P1 polytime reduces to P2, or

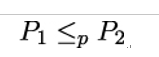
Informally, we can say that P2 is at least as hard as P1 ([117]). Now, the (hypothetical) algorithm A that can efficiently solve P2 is called an oracle for P2.

As an example, let P1 be the RSA-problem and P2 be the integer factorization problem. Recall from Chapter 7, Public-Key Cryptography, that the RSA problem means we have to find the plaintext m, given the ciphertext

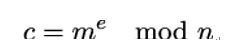
and the public key (e,n), while the integer factorization problems is to find the prime factors of a given integer.

Now it is easy to see that if we had an oracle that provides us with the prime factors of n in polynomial time, we could also solve the RSA problem, namely by computing the secret key d and then using d to decipher c. Thus, we have shown that

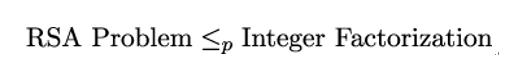
Surprisingly, the seemingly abstract concept of an oracle has important applications in various practical attacks on TLS. In this setting, you may think of an oracle simply as some technical system that is able to provide certain information that would not be available otherwise.

For example, old versions of the TLS Handshake protocol are susceptible to so-called padding oracle attacks when Alice and Bob use RSA-based key agreement. If RSA is used, Bob generates a 48-byte PreMasterSecret consisting of 2 fixed bytes describing the TLS protocol version and 46 random bytes as illustrated in Figure 20.3. Bob then encrypts that PreMasterSecret using the public RSA key from Alice’s certificate and sends the result to Alice in an encrypted message. Alice, in turn, decrypts Bob’s message and uses the PreMasterSecret to generate master˙secret, the secret used for computing TLS key material [5].

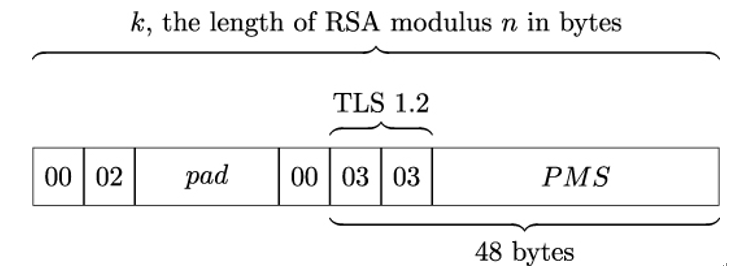
Figure 20.3: PKCS#1 padding used in TLS 1.2

Recall that TLS messages must be correctly padded according to PKCS #1 padding. But what does Alice do if the padding of a TLS message received from Bob is incorrect? In old TLS versions, Alice would, for example, send a bad TLS padding message, allowing Mallory to distinguish between correct and incorrect paddings.

These differences give rise to a padding oracle that Mallory can use to launch a padding oracle attack that completely compromises the TLS session’s security. In particular, Mallory chooses a large number of ciphertexts and determines the PreMasterSecret without the knowledge of Alice’s private RSA key – based on whether the individual plaintexts corresponding to Mallory’s chosen ciphertexts have valid PKCS #1 padding or not. Alternatively, Mallory can use this attack to forge Alice’s signature.

The first one to recognize this was the Swiss cryptographer Daniel Bleichenbacher. In 1998, Bleichenbacher published a paper describing chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS#1. Later on, his work became known simply as the Bleichenbacher attack.