18.4.1 Generating the Poly1305 key using ChaCha20

The Poly1305 key k can be generated pseudorandomly, for example, using the ChaCha20 block function. In this case, Alice and Bob need a dedicated 256-bit session key intended specifically for message authentication.

Generation of the authentication key (r,s) is done by computing the ChaCha20 block function with the following inputs:

• The 256-bit session integrity key that is used as the ChaCha20 key
• The block counter set to 0
• A 96-bit nonce that must be unique for every invocation of the ChaCha20 block function with the same key (therefore, it must not be randomly generated)

Computing the ChaCha20 block function produces a 512-bit state. Alice and Bob use the first 256 bits of the state as the one-time key for Poly1305. The first 128 bits are clamped and become part r, and the last 128 bits become part s. Algorithm 10 shows the Poly1305 key generation process as pseudocode.

  Algorithm 10: Poly1305 key generation process

Require: 256-bit key k, 96-bit nonce n
 Ensure: Generated key b
 ctr = 0
 b ← chacha20_block(k,ctr,n)
 return b0 … 31

ChaCha20 and Poly1305 can be also be used as building blocks within an AEAD construction.

18.5 ChaCha20-Poly1305 AEAD construction

ChaCha20-Poly1305 is a cryptographic algorithm for authenticated encryption with additional data (AEAD, see Chapter 15, Authenticated Encryption). Like the two building blocks ChaCha20 and Poly1305, ChaCha20-Poly1305 used in TLS is defined in RFC 8439 [131]. Initially, both building blocks were proposed by the American cryptographer Dan Bernstein [25, 23].

The ChaCha20-Poly1305 AEAD construction is illustrated in Figure 18.3. As you can see, the algorithm takes four inputs:

• A 256-bit shared secret key k
• A 96-bit nonce n, which must be different for each ChaCha20-Poly1305 algorithm invocation with the same key
• A plaintext p of arbitrary size
• Arbitrary-sized additional authenticated data d

In the first step, the Poly1305 one-time key kot is generated using the ChaCha20 block function B as described in Algorithm 10.

In the second step, the ChaCha20 encryption process C, discussed previously in this chapter and illustrated in Algorithm 8 is used to encrypt the plaintext p – using the shared key k and nonce n – with the counter ctr value initially set to 1.

In the last step, the Poly1305 algorithm P is executed using the previously generated one-time key kot and applied to a message obtained from concatenating the following data:

• Additional authenticated data d (recall this is optional data that is exempt from encryption)
• Padding 0p1 of up to 15 zero bytes so that the length of padded d is an integer multiple of 16 (if d’s length is an integer multiple of 16, 0p1 has the length of 0)
• The ciphertext c
• Padding 0p2 of up to 15 zero bytes so that the length of the padded ciphertext c is an integer multiple of 16 (again, if c’s length is an integer multiple of 16, 0p1 has the length of 0)
• The length of d in bytes len(d)
• The length of c in bytes len(c)

The output of the Poly1305 algorithm P is a 128-bit tag t that the receiving party will use to verify the integrity and authenticity of the received message, in particular, the received ciphertext c. The overall output of the ChaCha20-Poly1305 AEAD construction is, in turn, the pair (c,t), where c is the enciphered plaintext.

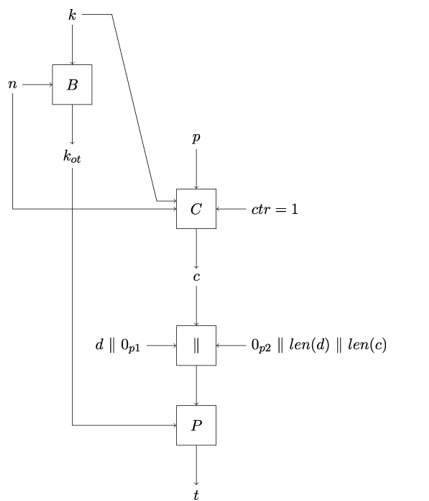
Figure 18.3: The ChaCha20-Poly1305 AEAD algorithm

Decryption using ChaCha20-Poly1305 is almost identical to encryption, except that:

• The ChaCha20 encryption algorithm C is now applied to the ciphertext c, thereby producing the original plaintext p (recall that for ChaCha20, encryption and decryption are identical operations)
• The inputs to the Poly1305 function P are as follows:
  • The padded authenticated data d ∥0p1
  • The received ciphertext c
  • The ciphertext’s padding
  • The length of c and the length of d: 0p2 ∥ len(d) ∥ len(c)
• Finally, the tag calculated by the receiving party is compared to the received tag, and the message is accepted only if the tags match

Note that one of the benefits of the ChaCha20-Poly1305 AEAD construction is that the same key is used for encryption and, effectively, message authentication (because the authentication key is derived from the encryption key using the ChaCha20 block function, as described in the previous section).