18.3 ChaCha20

ChaCha20 is a fast block cipher defined in RFC 8439 ChaCha20 and Poly1305 for IETF Protocols [131]. The number 20 in the cipher’s name refers to a specific ChaCha variant that uses 20 rounds or, equivalently, 80 quarter rounds to compute the ciphertext.

ChaCha20’s state is stored in a 4 by 4 matrix consisting of 32-bit unsigned integers. The state representation using a matrix explains why some ChaCha rounds are referred to as column rounds while others are referred to as diagonal rounds:

0   1   2   3
4   5   6   7
8   9  10  11
12  13  14  15

18.3.1 ChaCha20 quarter round

The ChaCha20 algorithm’s basic operation is the so-called quarter round. The quarter round operates on four elements of the ChaCha20 state, hence the name. The four elements are denoted as a, b, c, and d and the quarter round is defined as:

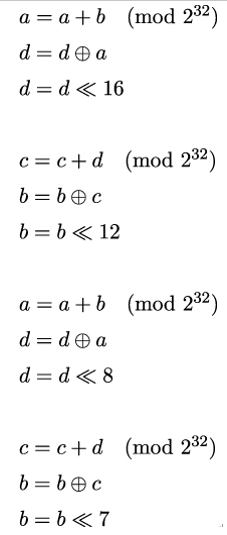
where ≪ n denotes the rotate left by n bits operation, for example:

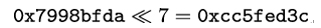
The ChaCha20 quarter round is illustrated in Figure 18.2. The illustration is based on the code in the TikZ for Cryptographers repository maintained by Jean Jérémy [90].

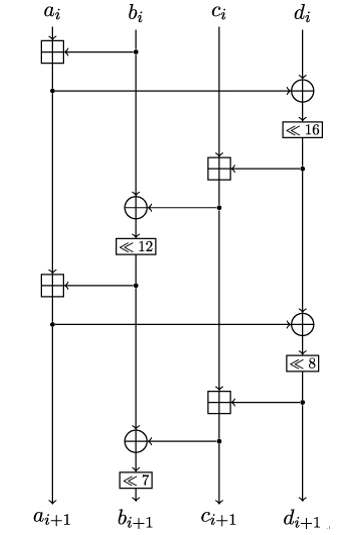
Figure 18.2: ChaCha quarter round

ChaCha20’s quarter-round operation is applied to four elements (32-bit unsigned integers) of the cipher’s state. So, since the algorithm’s state is a 4 by 4 matrix, the full ChaCha20 round requires four quarter rounds.

In RFC 8439, the quarter round is denoted by the function c—QUARTERROUND(x, y, z, w),— which takes the ChaCha20 state’s elements at indices x, y, z, and w.

For instance, if the function is called with the argument c—QUARTERROUND(1, 5, 9, 13)—, then the quarter round operation is applied to the state’s elements marked with an asterisk (and referred to as column round):
0   1*   2   3
4   5*   6   7
8   9*  10  11
12  13*  14  15

18.3.2 The ChaCha20 block function

The ChaCha20 block function takes the following as inputs:

• A 256-bit key
• A 96-bit nonce
• A 32-bit block count parameter

It transforms the cipher’s state by executing multiple quarter rounds, and produces a 64-byte pseudorandom output.

Before the round function can be applied, the ChaCha20 state is initialized as follows:

• The first four 4-byte words are set to constants 0x61707865, 0x3320646e, 0x79622d32, and 0x6b206574.
• The next eight 4-byte words are set to 4-byte chunks of the 256-bit ChaCha20 key, by reading the bytes in little-endian order, where the 12th word is a block counter. Because each block has 64 bytes, this 4-byte word is large enough for 256 GB of data.
• The last four 4-byte words are a nonce. The 13th word corresponds to the first 32 bits of the nonce taken as a little-endian integer, and the 16th word corresponds to the last 32 bits of the nonce. The nonce must be repeated for the same key.

With this, the initial value of ChaCha20’s state looks like this:

cccccccc  cccccccc  cccccccc  cccccccc
kkkkkkkk  kkkkkkkk  kkkkkkkk  kkkkkkkk
kkkkkkkk  kkkkkkkk  kkkkkkkk  kkkkkkkk
bbbbbbbb  nnnnnnnn  nnnnnnnn  nnnnnnnn

Here, c stands for the corresponding constant-, k for key-, b for block count-, and n for nonce-bytes.

After the initial state value has been set, ChaCha20 executes 20 rounds (80 quarter rounds) alternating between column and diagonal rounds. The column round is composed of the first 4 quarter rounds, and the diagonal round is composed of the last 4 quarter rounds:

QUARTERROUND(0, 4, 8, 12)
QUARTERROUND(1, 5, 9, 13)
QUARTERROUND(2, 6, 10, 14)
QUARTERROUND(3, 7, 11, 15)
QUARTERROUND(0, 5, 10, 15)
QUARTERROUND(1, 6, 11, 12)
QUARTERROUND(2, 7, 8, 13)
QUARTERROUND(3, 4, 9, 14)

After the 20 rounds are executed, the output words are added to the original input words (the addition is performed modulo 232), and the result is serialized by sequencing it in little-endian order.