19.7.1 Birthday attack
A birthday attack exploits the probability of collisions in a hash function – a mathematical property of such functions rooted in probability theory – in order to find two messages that have the same hash value.
Recall from Chapter 11, Hash Functions and Message Authentication Codes, that a secure cryptographic hash function must be second-pre-image resistant. That means, given message m and hash value h(m), the hash value of m computed using a cryptographically-secure hash function h, it must be computationally hard for Eve to find a second pre-image m such that h(m) = h(m).
Clearly, if Eve tries out enough different input messages for the hash function, collisions must occur at some point because h maps longer messages onto shorter messages. More precisely, if a given hash value h(m) is n bits long, then Eve can expect to find a second pre-image m after O(2n) trials. A second pre-image attack is therefore considered successful only if it has a significantly smaller complexity than O(2n).
A weaker form of attack occurs if Eve manages to find any collision, that is, any two messages m1,m2 with
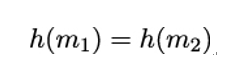
without reference to some given hash value. If it is computationally hard for Eve to construct any collisions, the hash function h is called strongly collision resistant.
As before, if Eve tries out enough different messages, collisions will naturally occur at some point, this time after about 2n∕2 trials. This much smaller number (compared to O(2n)) is a consequence of a phenomenon commonly known as the birthday paradox.
Consider a room with N people in it. Contrary to intuition, the probability of two people in the room having a birthday on the same day becomes larger than 0.5 as soon as N > 23. This is because the number of pairs P(N) that can be formed out of N people grows quadratically with N; more specifically, it is given by:
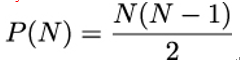
As a result, as soon as P(N) grows larger than 365, birthday collisions will occur with a high probability. This mathematical property can become a concern in a cryptographic setting if the hash function used by Alice allows Eve to find two distinct messages m,m′ that have the same hash value. For instance, if Alice has digitally signed m, Eve can append that signature to m′ claiming Alice has signed m′.
In a birthday attack, Eve picks messages m1,…,mq and computes their hash values h(m1),…,h(mq). Eve is said to be successful if she finds a pair of message mi, mj that leads to a collision for h. The birthday paradox implies that for a hash function h : {0,1}∗→{0,1}n having 2n possible hash values, collisions will occur after about 2n∕2 trials.
Consequently, an attack on strong collision resistance is considered successful only if it has a significantly smaller complexity than O(2n∕2). This also shows that, in general, hash functions with longer hash values can be considered to be more secure than hash functions with shorter hash values.
Leave a Reply